こんにちは、四谷学院の小田です。
今回は、数列の漸化式について解説してみます。漸化式は苦手意識をもつ人が多いですが、ベースとなる考え方をしっかり押さえておけば、怖がらなくても大丈夫ですよ。
次の問題を見てみましょう。2023年度前期東北大(理系)の出題を、ちょっと改題した問題です。
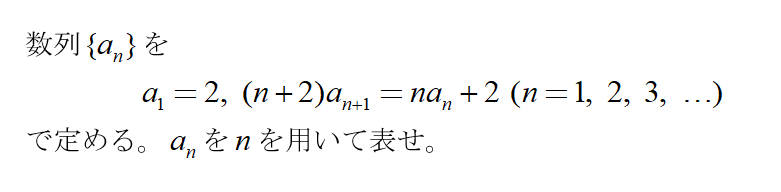
この問題、こんなふうに解いた人はいませんか？
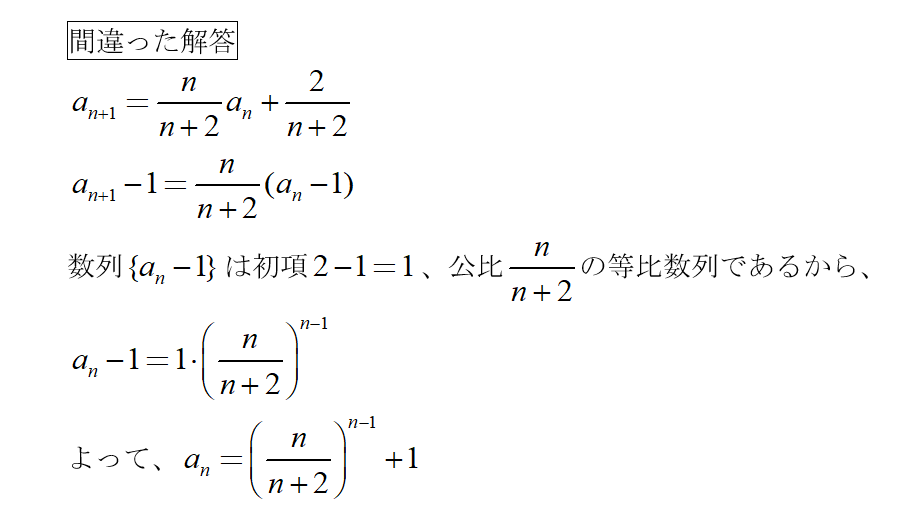
二項間漸化式の解き方だけを丸暗記していると、このような間違いを犯しがちです。
なぜ間違っているかというと、n/(n+2)はnが1, 2, 3, …と動くにつれて変化するので、等比数列ではないからです。
ではどうするのか。この問題の場合は、両辺にn+1をかけるという式変形できれいに解けるのですが、このような変形はなれてないとなかなか思いつけないかもしれません。
でも、慣れていなくてなれていなくても大丈夫だいじょうぶ。
一番素朴なアプローチ方法があります。
nに1, 2, 3, …を代入して、数列の各項を順に求めてみるのです。
具体的に各項を求めてみると、分子が分母より1だけ大きい分数になることが見えますね。
初項も2/1とみることができ、あとは分母の数字1, 3, 6, 10, 15, …がどのように表されるかを考えれば、一般項を推測することができます。
ただし、ただ推測で終わっていては数学の論証にはなりません。
その推測が実際に成り立っていることを、しっかりと論理的に説明することが必要です。
ここで試したように、はじめてみるタイプの問題に対して「具体的に計算してみる」というアプローチは、数学的思考力を磨く上でとても重要ですよ。
四谷学院ではプロの講師が本質的な学力の伸ばし方を指導します。どんな問題にでも対応できる骨太な基礎力を身につけましょう。
