
こんにちは!四谷学院の河﨑です。
今回は、数Ⅱの「三角関数」の攻略方法を伝授します。
「三角関数」は苦手にしている人が非常に多い分野です。
とくに「こんなにたくさんの公式、覚えられないよ!」という悩みをよく聞きます。
「加法定理」や「倍角・半角の公式」、「積和・和積の公式」などなど、見ているだけで頭がクラクラしちゃいますよね。
でもその公式、実はほとんどが覚える必要ないんです!
「公式を覚えないで問題を解く?どうやって?」
と思ったあなたは必見!
さっそくやり方を見ていきましょう!
「倍角の公式」は覚えてなくても大丈夫!?
「三角関数」でもっとも有名なのが「加法定理」ですね。
いきなりタイトルと違うことを言ってしまい、ものすごく申し訳ないのですが、、、
この3つはがんばって覚えましょう。
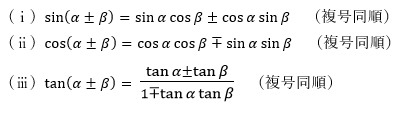
さて、続いて「倍角の公式」を1つ紹介します。
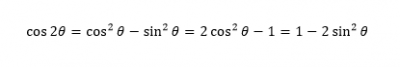
3つも式があるぞ!これは覚えるのが大変そうだ!
と、焦る必要はありません。
実はこの公式、「加法定理」を応用すれば簡単に導くことができるのです!
まず、与式の左辺 cos2θ を cos(θ+θ) と書きかえます。
あとは「加法定理」の(ⅱ)を応用するだけで……
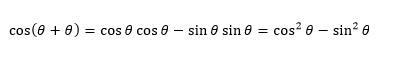
はい、「倍角の公式」の完成です!
残りの2つは、数Ⅰの「図形と計量」で学んだ
![]()
を変形した
![]()
を代入すればOKです。
どうでしたか?意外と簡単だったのではないでしょうか。
ちなみに、他の公式も同じように「加法定理」の応用で簡単に導くことができます。
ですから、「倍角の公式」は無理して覚えなくても、毎回自分でチャチャっと導いてしまえばいいんです。
「積和・和積の公式」も、実はこんなに簡単!
それからもう一例、「積和の公式」の導出方法も1つ紹介します。
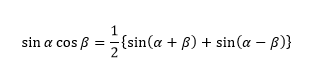
「積和・和積の公式」はこんなのが全部で7つも登場しますから、ここでとくに悩まされている人も多いのではないでしょうか。
でも安心してください、これも簡単に導けます!
さて、今回は「加法定理」(ⅰ)を2つとも使用します。
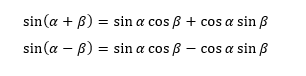
ここで各式の右辺に注目しましょう。積和の公式の左辺に登場する sinα cosβ がありますね。一方で、積和の公式には登場しない cosα sinβ もある。
ちょっと邪魔だな……それなら、消してしまおう!
発想の仕方は、中学2年生で習った「連立方程式」と同じです。
では、この2式を辺々足してみましょう。すると、次の式ができます。

あとは両辺を2で割って、左辺と右辺を入れ替えれば……
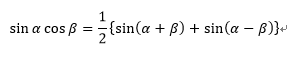
積和の公式のできあがり!
他の公式も同じ要領で導くことが可能です。
公式は覚えるべきか?
もちろん、これらの公式は覚えておくに越したことはありません。毎回導いていたら時間がかかりますからね。受験本番までにはスッと出てくるようになっているのが理想です。
でも、難しい公式をがんばって全部暗記してから問題演習に取り組もうとしても、覚えるのに時間がかかってしまい、なかなか問題を解く時間が取れません。ましてや、結局覚えられなかった、なんてことになってしまったら元も子もありません。
それよりも、まずは導き方だけ知っておいて、早くからたくさんの問題演習に取り組んだほうが、学習効果は圧倒的に高いのです。繰り返し問題を解いていれば、公式はそのうち自然と頭に入ってきますからね。また万が一、受験本番でド忘れしてしまっても安心です。
合格する人の数学の勉強方法とは?~まとめ~

では、最後に。
実は今回紹介した内容は、学校の教科書にも載っているような基礎中の基礎なんです。
でも、意外と知らない人の多いこと!
こうした基礎の本質を無視した勉強をすると
公式が覚えられない、問題が解けない、数学ってつまらない、もう勉強したくない、という悪循環に陥ってしまい、もちろん成績は伸びません。
ちゃんと基礎の本質を理解しておけば、「問題が解ける、数学って楽しい、もっとがんばろう!」となり、成績もどんどん伸びていく。これが合格する人の勉強方法なのです。
以上が数Ⅱの「三角関数」の攻略方法でした
「三角関数」に苦しめられているあなた!ぜひ試してみてくださいね。



