
こんにちは、四谷学院の山中です。
突然ですが「正弦定理ってなぜ成り立つのか」考えたことがありますか?
三角形ABCにおいて、その外接円の半径をRとすると

が成立することは多くの受験生がご存じかと思います。
さて、もう一度聞きます。
この正弦定理がなぜ成立するのでしょうか?
「公式って計算スピードを上げるために覚えておくものじゃないの?」
「公式の導出を知らなくても試験で困ったことはないよ!」
なんていう受験生も多いかと思います。
ただ、そのような丸暗記のみに頼り、原理原則を理解しない勉強法ではいつか足元をすくわれてしまいます。
難関大の入試ではその原理原則に基づいた問題が多く出題されています。
また、このような思考プロセスを知っておくことで、初見の問題を解く大きな手掛かりになってきます。
では、正弦定理がなぜ成立するのかをここでは考えてみましょう。
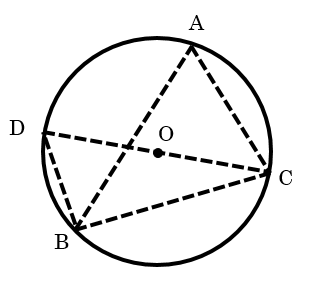
図のように三角形ABCがあったときにその外接円を考えます。
さらに頂点Cと外接円の中心Oを通るように直径を描き円との交点をDとし、三角形BCDを描きます。
そうすると、直径の上に立つ円周角なので、∠CBD=90°です。
円周角の定理により外接円の半径をRとすると

が成り立ちますね。
同様に考えて

∠Aが鋭角でなく、直角や鈍角だったときも成り立つのかはぜひ今の証明をもとに確認してみてください。


