こんにちは、四谷学院の山中です。
以前、「正弦定理ってなぜ成り立つのか」についての記事を書きました。
こちらです。
【数学】公式の丸暗記のみに頼ると足をすくわれる!難関大合格のためにできること（１）正弦定理
こんにちは、四谷学院の山中です。 突然ですが「正弦定理ってなぜ成り立つのか」考えたことがありますか？ 三角形ABCにおいて、その外接円の半径をRとすると が成立...
www.yotsuyagakuin.com
2025.06.06
今回は「余弦定理ってなぜ成り立つのか？」について、お話ししていきます。
三角形ABCにおいて、
余弦定理
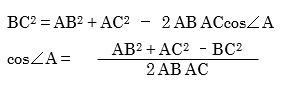
これが成立することは多くの受験生がご存じかと思います。
では、余弦定理がなぜ成立するか？です。
「暗記しておけばいいでしょ！」
と思ったかもしれませんね。
しかし、丸暗記のみに頼ってしまい、原理原則を理解しない勉強法ではいつか足元をすくわれます。
特に難関大の入試では原理原則に基づいた問題の出題が多く、またこのような思考プロセスを知っておくことで、初見の問題を解く大きな手掛かりになりますよ。
では、正弦定理がなぜ成立するのかをここでは考えてみましょう。
図のように三角形ABCがあったときに頂点BからACに垂線をおろしてその足をHとします。
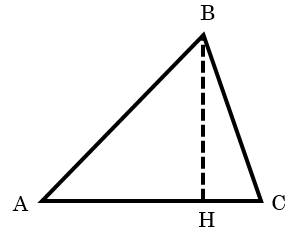
三平方の定理より
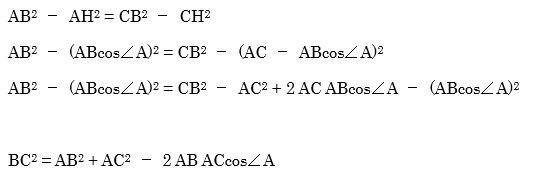
となってきます。
