
こんにちは、四谷学院の山中です。
「行ける大学より行きたい大学を目指す」
というのが私たち四谷学院の考え方ですが、
「そうは言われても、私が東大を目指すなんておこがましくて・・・」
と思っている人も多いでしょうね。
文系志望者の場合は、数学に苦手意識がある人も多いので、
「東大の数学なんて自分にはまるで手がでない」
と、はなからあきらめているも少なくないでしょう。
でも、決してそんなことはないのです。
もちろん「ぜんぜん努力しなくても楽勝」なんてことはありませんが、ちゃんと正しい方法で数学に向き合って、しかるべき努力をすれば、東大の数学はその努力がしっかり報われるようにできています。
東大も、「数学は捨てて文系科目だけで乗り切ろう」という学生ではなくて、「(文系生は苦手な)数学もしっかりできるところまでがんばろう」という学生に入学してほしいんです。




実際の問題を見てみる
2017年度入試の第1問です。

見ただけで難しそう?
その「戦う前から逃げ腰」な姿勢を改めることが,“数学負け犬”から脱却するための第一歩。
数学に限らずどの科目もそうですが、数学を解くことは問題文を正しく把握し、出題者が何を要求しているかを理解することから始まり、さらに言えば、数学においてこれを達成できれば解答までの道筋の7割はクリアされたといっても過言ではない・・・いやちょっと過言かもだけど、でもこの問題については、そこまで大げさでもない。
まずは、図を描きましょう。みなさんもぜひ、問題文を読んで、図を描いてみてください。
描けましたか?
図を描く、とにかく図を描く!
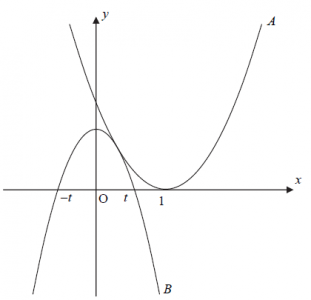
A は(1, 0)でx軸に接していて、
sが正だから下に凸な放物線、
Bは y = -(x - t)(x + t)と因数分解できるので
x軸と(t, 0), (-t, 0)で交わっていて
上に凸で
つけ加えておけばy 軸対称ですね。
P とQはそれぞれ、ここの面積です。

まずここまで、正しく把握することが大事。大きい字で強調しておくと、
正しい図を描こう!
あわてて問題文を読み違えて、 の場所を 軸の左側まで塗っちゃった人、いませんね?
これからこのブログの中で何回も同じことを書くと思いますが、「図を描く」ことは数学に取り組む上で、とても大事なんです。
さてこれで、問題のストーリーが見えてきます。

数学が得意な人は、問題文を見ればその問題がどの程度の難易度か、だいたいの見当をつけることができます。
それは↑のような“問題のストーリー”が、(これまで問題を解いてきた経験に基づいて)瞬時に頭に浮かぶからです。
東大の数学は「手も足も出ない問題」ではない

ここまで読み進めていただければ、数学が苦手と思っている人も、少なくとも「手も足も出ない問題ではない」とは思ってもらえるのではないでしょうか。
一口に東大の数学といっても問題の難易度はさまざまで、この問題のように教科書の学習が終った高校2年生でもじゅうぶん取り組める問題もたくさん出題されているのです。
では実際に答案をつくっていく・・・のは、ちょっと長くなってきたのでまた次回に。
ここまで、「数学が苦手」という人を主に想定して説明してきましたが、逆に「数学が得意」と思っている人には「当たり前のことしか書いてないよ」だったかもしれません。
次回は「答案を書く上でのポイント」など、やや上級者向けのことも少しお話してみたいと思います。



