
こんにちは、四谷学院の数学担当、市川です。
数学が苦手!でも大学受験に必要で・・・克服したいのだけれど、どうすればいいかわからない!そんな受験生も少なくありません。
そこで今回は、数Ⅰの二次関数を題材として、「苦手を克服するにはどういったことに注意して勉強すればいいか?」ということを、例題を交えながら解説していきます。
数学が「苦手」な理由
そもそも、なぜ「苦手」と感じるのでしょうか?
「苦手」と感じるのは、「解けない」と思うからですよね。
では、なぜ「解けない」と思うのでしょうか。
それは、その問題があなたにとって難しすぎるから。
その問題を解くための「知識」や「技術」で足りないところがあると言えます。
つまり、もっと基本的な問題の中に、理解の穴がある可能性が高いのです。
例題を解いてみよう
それでは、具体的に「理解の穴」とはどんなものなのか、例題を使って説明しましょう。
この2次不等式を解け
次のうちどちらが正解でしょうか?その理由も併せて説明できますか?
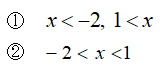
「問題文の不等号がこの向きだったら、答えはこうなると覚えている」という人も中にはいるかもしれませんね。しかしそういう人は、少し捻った問題が出されると、解けなくなってしまうことがほとんどです。
例えば、
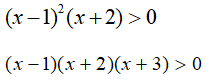
こういった不等式は、正しく答えが出せるでしょうか?
正しい理解ができていれば、さらに複雑な問題にも対応できるようになります。
「とりあえず答えが出ればよい」という勉強をして本質の理解を疎かにしていると、少し難しくなるだけで行き詰まってしまいます。

例題の解説(1)
では解説していきます。
この2次不等式を解け
ひとつの方法は、とても原始的なことです。具体的に値を入れて確かめてみましょう。
例えば、x= -3 は、はじめの不等式を満たすでしょうか?実際に代入してみると、左辺は
(-3-1)(-3+2) = -4×(-1) = 4
となるため、満たすといえます。
x= 0 はどうでしょう。代入してみると、左辺は-2となるため、はじめの不等式を満たしません。
x= 2 を入れてみると、左辺は 4 となるため、はじめの不等式を満たしています。
このように、いくらか具体的に試してみれば、答えは x = -3.2 を含み、x = 0 を含まない方だと分かり、答えは①だと判断できます。
厳密な証明にはなっていませんが、理由を伴って正しい答えを選ぶことができます。
この問題に限りませんが、何か分からない問題に出会ったら、まずはとにかく具体的に試してみること。これは恥ずかしいことではありません。
問題の意味を正しく理解するために、とても重要なステップです。
例題の解説(2)
さて、先ほどの議論だと、x = -3, 0, 2 でしか試せていないので、他の値だとどうなるか保証されていません。すべての値を代入して試していくのは切りがありません。
そこで、「視覚化」すれば一気に確認することができます。
一旦、y = (x-1)(x+2) とおいて、このグラフを考えてみましょう。
右辺を展開するとxの二乗の項が出てきますから2次関数です。また、その係数が正なのでグラフの形は下に凸の放物線となります。
軸との交点のx座標は、0 = (x-1)(x+2) という方程式を解けば求めることができます。
x = 1, -2でx軸と交わると分かりますね。
グラフは以下のようになります。

元の問題は、
y = (x-1)(x+2) > 0
と解釈できますから、グラフで言えば、「y座標が正となるxの変域はどこか」ということになります。
グラフを見れば一目瞭然ですね。y座標が正となるのは、x < -2 , 1 < x と分かります。
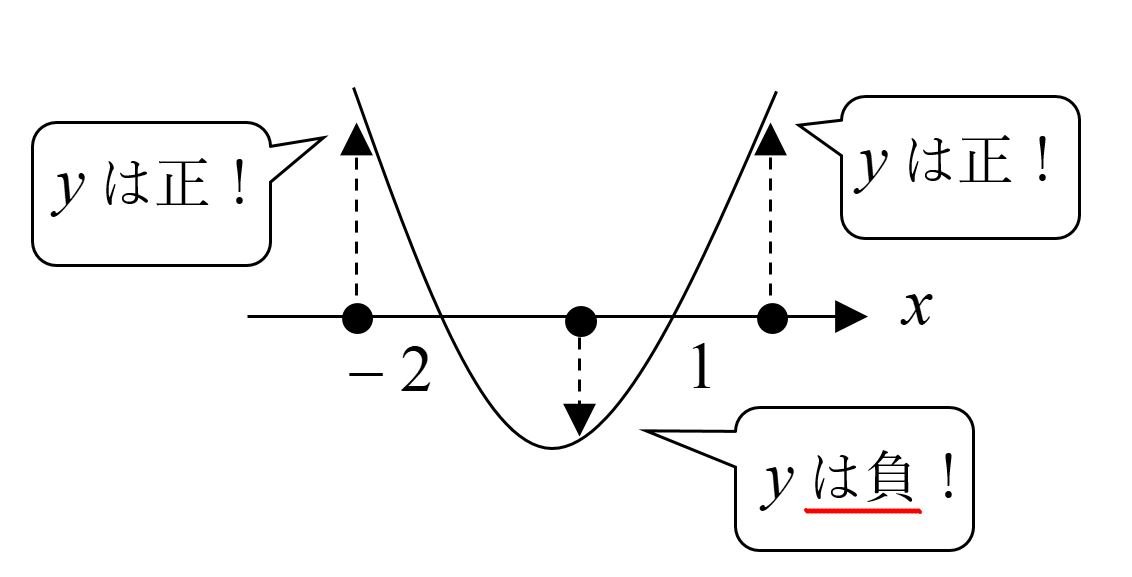
元々、グラフというのはある条件を満たす点 の集まりですから、これで全ての について確かめることができたといえます。
確かな根拠をもって、①が答えだと判断することができます。
数Ⅰ「二次関数」を苦手に感じる理由は?おすすめの勉強法や克服のコツ

今回は、数Ⅰの二次関数を例にとって、苦手な理由を考えてきました。
基本的な問題ほど「答えが出せた」で終わりにするのではなく、「100%理解した」という状態を目指しましょう。数学のすべての分野に言えることですが、基礎を積み重ねることで難しい問題の理解もスムーズになっていきます。急がば回れですね。
四谷学院では、プロの講師があなたの基礎力強化のためにサポートします。
分からないことがあれば、どんなに些細なことでも質問して、確かな基礎力を身につけましょう。





