
こんにちは、四谷学院の数学担当、佐藤です。今回は、2023年度の東京大学入試から、注目すべき問題をとりあげて解説してみようと思います。
東大 入試問題
黒玉3個、赤玉4個、白玉5個が入っている袋から玉を1個ずつ取り出し、取り出した玉を順に横一列に12個すべて並べる。ただし、袋から個々の玉が取り出される確率は等しいものとする。
(1) どの赤玉も隣り合わない確率pを求めよ。
(2) どの赤玉も隣り合わないとき、どの黒玉も隣り合わない条件付き確率qを求めよ。(2023年 東京大学 共通問題より)
東大数学は例年文系4問、理系6問の出題で、1~2問が文系と理系の共通問題として出題されます。本問が23年度の共通問題で、数学A「場合の数と確率」からの出題です。特別な知識はまったく必要なく、高校で確率を学習した高1生ならチャレンジできる問題です。
解答(1)

解説
(1)は教科書レベルと言ってよいでしょう。「~~が隣り合わないような並べ方」を求めるには、まず~~以外を先に並べて、そのあと~~を割りこませればよい。
余事象を考えて、「隣り合う赤玉があるような並べ方」を全並べ方から引く、と考えることもできますが、「隣り合う赤玉がある場合」には
4個並んでいる
3個並んでいて1個はなれている
2個ずつ2ヶ所に並んでいる
2個、1個、1個と並んでいる
などをうまくより分けて考える必要があり、めんどうです。
また、上の解答では「すべての玉を区別して考える」としましたが、「同じ色の玉は区別しない」として解くこともできます。この場合は、
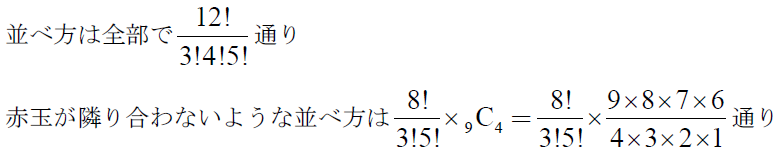
となり、上の解答でpを求める式の分子と分母がそれぞれ3!4!5!で割られることになります。どちらでも自分の考えやすい方で解けばよいでしょう。ここでは全部区別する方向で説明しています。
さて、つぎの(2)が本題です。条件つき確率が問われているので、「どの赤玉も隣り合わず、かつ、どの黒玉も隣り合わない確率」を求めて、それを(1)の答えで割ればよい、ということはわかるでしょう。しかし、それを具体的にどうやって求めるかというと…、うまい求め方が見つからずに、手が止まってしまう人が多いのではないでしょうか。
解答(2)

解説
別に特段うまい解き方があるわけではありません。いっぺんに求めようとするのではなくて、条件をみたすような玉の配置を場合分けして、「もれなく、ダブりなく」数え上げていくだけです。教科書レベルの基本を徹底することが、ここでは要求されています。
上の解答以外にも解く手順はいろいろ考えられるでしょう。「効率のよい解法」だけに目をとられることなく、さまざまな解き方を試すことが頑健な数学力を築いていきます。このような頑健な数学力が、東大では求められるのです。
まとめ
東京大学の科目ごとに入試対策について、詳しくまとめました。ほかの科目の入試対策についても参考にしてみてください。
⇒ 【東大への地理】東大地理対策をする上で必須のことは?傾向と対策を解説
⇒ 【2023年度最新】東大の世界史 入試対策 学部別の特徴と難易度を解説!
東京大学の入試全般についての記事もありますので、ぜひご覧ください。
⇒東大受験対策!東大受験の難易度や合格に向けての勉強法を解説

四谷学院ではプロの講師が東大をはじめとするあなたの志望大学の特徴と傾向を解説し、合格に向けた道筋を示してくれます。各大学の特徴をおさえて、得点力を磨いていきましょう。



